Clustering¶
Clustering is grouping a set of objects such that objects in the same group (i.e. cluster) are more similar to each other in some sense than to objects of different groups.
To exploit data for diagnostics, prediction and control, dominant features of the data must be extracted. In the opening chapter of this book, SVD and PCA were introduced as methods for determining the dominant correlated structures contained within a data set. In the eigenfaces example of Sec. 1.6, for instance, the dominant features of a large number of cropped face images were shown. These eigenfaces, which are ordered by their ability to account for commonality (correlation) across the data base of faces was guaranteed to give the best set of r features for reconstructing a given face in an l2 sense with a rank-r truncation. The eigenface modes gave clear and interpretable features for identifying faces, including highlighting the eyes, nose and mouth regions as might be expected. Importantly, instead of working with the high-dimensional measurement space, the feature space allows one to consider a significantly reduced subspace where diagnostics can be performed.
K-means algorithm¶
The term “k-means” was first used by James MacQueen in 1967, though the idea goes back to Hugo Steinhaus in 1957. Our specific clustering problem:
Given: a set of 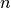 observations
observations 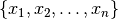 , where each observation is a d-dimensional real vector
Given: a number of clusters
, where each observation is a d-dimensional real vector
Given: a number of clusters 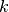 Compute: a cluster assignment mapping
Compute: a cluster assignment mapping 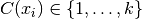 that minimizes the within cluster sum of squares (WCSS):
that minimizes the within cluster sum of squares (WCSS):
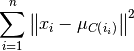
where centroid 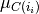 is the mean of the points in cluster
is the mean of the points in cluster 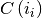 .
.
General algorithm goes like this:
Randomly choose 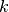 cluster centroids
cluster centroids 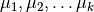 and arbitrarily initialize cluster assignment mapping
and arbitrarily initialize cluster assignment mapping  .
While remapping
.
While remapping  from each 𝒙_𝑖 to its closest centroid
from each 𝒙_𝑖 to its closest centroid 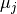 causes a change in
causes a change in 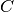 :
Recompute
:
Recompute 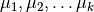 according to the new
according to the new 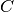
In order to minimize the WCSS, we alternately:
Recompute 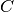 to minimize the WCSS holding
to minimize the WCSS holding 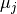 fixed.
Recompute
fixed.
Recompute 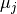 to minimize the WCSS holding
to minimize the WCSS holding 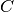 fixed.
fixed.
In minimizing the WCSS, we seek a clustering that minimizes Euclidean distance variance within clusters.