Matrices¶

What is a Matrix?¶

This lesson introduces the matrix - the rectangular array at the heart of matrix algebra. Matrix algebra is used quite a bit in advanced statistics, largely because it provides two benefits.

Compact notation for describing sets of data and sets of equations. Efficient methods for manipulating sets of data and solving sets of equations.

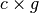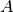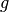In general, the data from single-cell transcriptomics can be described in a $c \times g$ expression matrix $A$ , where $c$ is the number of cells, $g$ is the number of genes, and the element 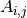$A_{i,j}$ indicates the expression of gene 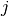$j$ in cell 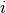$i$ . As the human body expresses about 20,000 genes ( 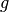$g$ ≈ 20,000), the cells are embedded in a high-dimensional transcriptional space in which cells are close to each other if they have a similar expression of genes.

Matrix Definition¶

A matrix is a rectangular array of numbers arranged in rows and columns. The array of numbers below is an example of a matrix.

$n_{\mathrm{offset}} = \sum_{k=0}^{N-1} s_k n_k$

The number of rows and columns that a matrix has is called its dimension or its order. By convention, rows are listed first; and columns, second. Thus, we would say that the dimension (or order) of the above matrix is 3 x 4, meaning that it has 3 rows and 4 columns.

Numbers that appear in the rows and columns of a matrix are called elements of the matrix. In the above matrix, the element in the first column of the first row is 21; the element in the second column of the first row is 62; and so on.

Matrix Notation¶

Statisticians use symbols to identify matrix elements and matrices.

Types of Matrices¶

This lesson describes a few of the more important types of matrices: transpose matrices, vectors, and different kinds of square matrices.

The transpose of one matrix is another matrix that is obtained by using rows from the first matrix as columns in the second matrix.

For example, it is easy to see that the transpose of matrix A is A’. Row 1 of matrix A becomes column 1 of A’; row 2 of A becomes column 2 of A’; and row 3 of A becomes column 3 of A’.

A square matrix is an n x n matrix; that is, a matrix with the same number of rows as columns. In this section, we describe several special kinds of square matrix.

Advanced matrix concepts¶

https://docs.microsoft.com/en-us/azure/quantum/concepts-advanced-matrices

Eigenvalues and eigenvectors¶

Matrix exponentials¶

A matrix exponential can also be defined in exact analogy to the exponential function. The matrix exponential of a matrix 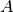$A$ can be expressed as

https://docs.microsoft.com/en-us/azure/quantum/concepts-vectors-and-matrices

The Geometry of Matrix Multiplication¶

Norm¶

https://medium.com/towards-artificial-intelligence/basic-linear-algebra-for-deep-learning-and-machine-learning-ml-python-tutorial-444e23db3e9e#60ee

Dot product¶

Eigenvalues & Eigenvectors¶

Matrix Multiplication¶

Mr. David DeSalvo, Chaplain at St. Andrew’s School https://www.linkedin.com/in/david-desalvo-129aa834/ Precalculus Honors (December 7, 2005). Applications of Matrix Multiplication.

The Sandwich Problem¶

Suppose you and your roomate go into partnership making sandwiches to sell in your dormito1y. Suppose that each of you makes 3 different types of sandwiches.

Sandwich 1: made of bread, peanut butter, and jelly
Sandwich 2: made of bread, ham, and cheese
Sandwich 3: made of bread, cheese, and tomato

Each night, you ( $y$ ) and your roommate ( $r$ ) plan to sell a number of sandwiches of each kind shown in matrix $A$ .

$A$

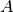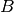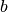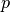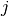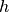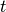Each sandwich is made by putting together some combination of slices of bread, peanut butter, jelly, ham, cheese, and tomato. Matrix $B$ describes the number of pieces of bread ( $b$ ), ounces of peanut butter ( $p$ ), ounces of jelly ( $j$ ), slices of ham ( $h$ ), slices of cheese ( $c$ ), and slices of tomato ( $t$ ) needed for each kind of sandwich.

$B$

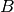
To determine the ingredients for each sandwich you need to make in matrix 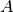$A$ , we will examine the following questions.

1. How many slices of bread will you use to make the sandwiches?

You will make 4 Sandwich 1 sandwiches, each of which uses 2 slices of bread; 5 Sandwich 2 sandwiches, each of which uses 2 slices of bread; and 3 Sandwich 3 sandwiches, each of which uses 2 slices of bread. The total number of slices of bread you will use is expressed by the sum of the products

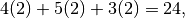
$4(2) + 5(2) + 3(2) = 24,$

so you need 24 slices of bread.

1. How many slices of bread will your roommate use to make the sandwiches?

Your roommate will make 3 Sandwich 1 sandwiches, each of which uses 2 slices of bread; 3 Sandwich 2 sandwiches, each of which uses 2 slices of bread; and 3 Sandwich 3 sandwiches, each of which uses 2 slices of bread The total number of slices of bread your roommate will use is exp,ressed by the sum of the products

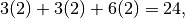
$3(2) + 3(2) + 6(2) = 24,$

so your roommate also needs 24 slices of bread.

1. How much peanut butter will you use?

The amount of peanut butter you will use is

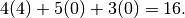
$4(4) + 5(0) + 3(0) = 16.$

You will use 16 ounces of peanut butter.

1. How much jelly will you use?

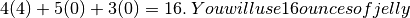
$4(4) + 5(0) + 3(0) = 16. \: You will use 16 ounces ofjelly$

1. How much ham will you use?

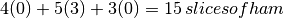
$4(0) + 5(3) + 3(0) = 15 \, slices of ham$

1. How much cheese?

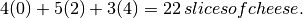
$4(0) + 5(2) + 3(4) = 22 \, slices of cheese.$

1. How much tomato?

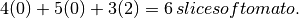
$4(0) + 5(0) + 3(2) = 6 \, slices of tomato.$

Similarly, your roommate will use (in addition to the 24 slices of bread)

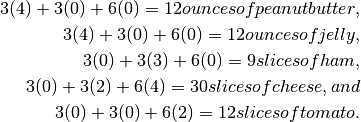
$3(4) + 3(0) + 6(0) = 12 ounces of peanut butter, \\ 3(4) + 3(0) + 6(0) = 12 ounces of jelly, \\ 3(0) + 3(3) + 6(0) = 9 slices of ham, \\ 3(0) + 3(2) + 6( 4) = 30 slices of cheese, and \\ 3(0) + 3(0) + 6(2) = 12 slices of tomato.$

We can summarize the amount of each ingredient with the following matrix C, in which the entries are the numbers of ounces or slices of food.

$A$

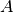
Observe that the entiy in the first row and first column of C is obtained by lining up the first row of A and the first column of 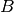$B$ , then multiplying the coITesponding entries and adding the products together. Row 1 of 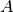$A$ and column 1 of 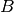$B$ are

$B$

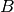
Multiplying pairwise term by term gives

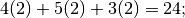
$4(2) + 5(2) + 3(2) = 24;$

this sum is entiy 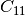$C_{11}$ . Likewise C2s is obtained by multiplying pairwise term by term the second row of 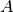$A$ by the fifth column of 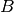$B$ , as shown below.

$B$

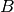
What row of A multiplied by what column of B gives entry C12? The entry in the row and second column ofC is found by multiplying the first row of A by the second column of B.

$B$

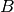
All of the entries in C can be found using the method illustrated above. This way of combining entries in two matrices to yield a third matrix is called matrix multiplication; matrix C is defined as the product of matrices A and B. The operation can be written in the fo1m shown below.

$C=A*B$

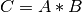
In general, the matrix multiplication 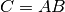$C=AB$ is defined as follows: Each entry 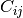$C_{ij}$ is obtained by multiplying pairwise te1m by term the ith row of the left-hand matrix 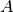$A$ by thejth column of the right-hand matrix 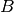$B$ . In symbols, this definition means that

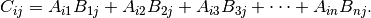
$C_{ij} = A_{i1}B_{1j} + A_{i2}B_{2j} + A_{i3}B_{3j} + \cdots + A_{in}B_{nj}.$

https://xaktly.com/MatrixOperations.html

https://link.springer.com/chapter/10.1007/978-981-10-6808-9 _1 -

https://julienbeaulieu.gitbook.io/wiki/sciences/math/linear-algebra/operations -

Matrices as Transformations¶

https://youtu.be/evGm6IJKrDI?t=1217

Eigenvectors of Matrices¶

We have seen that multiplying a vector by a matrix results in a vector:

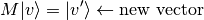
$M|v\rangle = |v'\rangle \leftarrow \text{new vector}$

If we chose the right vectors and matrices, we can find a case in which this matrix multiplication is the same as doing a multiplication by a scalar:

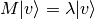
$M|v\rangle = \lambda|v\rangle$

(Above, 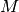$M$ is a matrix, and 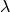$\lambda$ is a scalar). For a matrix 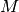$M$ , any vector that has this property is called an eigenvector of $M$ .

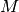In this chapter, you will discover the eigendecomposition, eigenvectors, and eigenvalues in linear algebra. After completing this tutorial, you will know: What an eigendecomposition is and the role of eigenvectors and eigenvalues. How to calculate an eigendecomposition in Python with NumPy. How to confirm a vector is an eigenvector and how to reconstruct a matrix from eigenvectors and eigenvalues. This tutorial is divided into 5 parts; they are: Eigendecomposition of a Matrix, Eigenvectors and Eigenvalues, Calculation of Eigendecomposition, Confirm an Eigenvector and Eigenvalue, Reconstruct Original Matrix Transpose a vector Find The Maximum And MinimumDescribe An ArrayCreate A VectorCreate A Sparse Matrix

https://textbooks.math.gatech.edu/ila/overview.html - Most engineering problems, no matter how complicated, can be reduced to linear algebra:

https://stats.stackexchange.com/questions/281162/scale-a-number-between-a-range https://stats.stackexchange.com/questions/178626/how-to-normalize-data-between-1-and-1

function dataNormalized=normalizeData(data)
    %Normalize Sample Data
    dataNormalized=zeros(size(data));
    for j=1:size(data,2)
    dataNormalized(:,j)=(data(:,j)-min(data(:,j)))/( max(data(:,j))-min(data(:,j)) );
    end
end

https://en.wikipedia.org/wiki/Feature _scaling

Normalization rescales the values into a range of [0,1]. This might be useful in some cases where all parameters need to have the same positive scale. However, the outliers from the data set are lost.Xchanged=X−XminXmax−XminStandardization rescales data to have a mean (μ) of 0 and standard deviation (σ) of 1 (unit variance).Xchanged=X−μσ

Linear independence¶

https://www.youtube.com/watch?v=xfhzwNkMNg4 -

Inverse of a 3x3 Matrix using Adjoint¶

https://www.youtube.com/watch?v=xfhzwNkMNg4 -

https://www.youtube.com/watch?v=HYWeEx21WWw -

Transpose A Vector Or Matrix

[Selecting Elements In An Array](https://chrisal