Decomposition

A “component” is a single part of something larger. For instance, an engine is a component of a car and a piston is a component of an engine. An object’s “composition” is everything that makes up the object. So, we can say that the engine, pistons, aluminum, steel, and paint are “components” that make up the car’s “composition.” As nouns the difference between composition and component is that composition is the proportion of different parts to make a whole while component is a smaller, self-contained part of a larger entity often refers to a manufactured object that is part of a larger device. As an adjective component is making up a larger whole; as a component word.

Eigendecomposition

In linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors.

Singular Value Decomposition (SVD)

https://www.youtube.com/watch?v=EokL7E6o1AE

this week we are changing topics to I’m going to go out and say it is the most important week of the class what you learn here is one of the most important tricks of the trade it’s called I’m going to write it up on the board the singular value decomposition this week’s lecture is focused on this is going to basically introduce through this really amazing data analysis tool it’s all in your algebra as always but what you can do with this is quite remarkable so in this first lecture I’m going to introduce you to the singular value decomposition and by the end of this week I’m going to show you how you can use this to do things like start thinking about how you might do image recognition software for faces for classification dogs versus cats and all kinds of interesting ideas that come out of this singular value decomposition extremely powerful extremely useful in a lot of contexts and so let’s begin and let’s start thinking about what this thing is so first off let’s think about

what linear algebra does and what a matrix does to a vector okay I’m going to take as an example the following vector 1 3 ok I’m going to show you all the ideas in two-dimensional space and then we’re going to generalize a tire dimensional space and I’m going to take a matrix a which is just a following I’ll just make this stuff up ok so I take these two things and what I want to do is think about constructing a vector Y which just says simply a times X so this is just a you know a matrix times this vector it’s a simple procedure we’ve been doing this all quarter and what does it give you well if you do this multiplication now right this times this which is 2 plus 3 this times this that’s a negative 1 plus 3 2 simple no magic very a straightforward idea but let’s start thinking about what this does graphically so let me draw sort of our typical Cartesian coordinates and if you notice the vector 1 3 right so if you go over in some coordinates here vector 1 3 is sort of a vector that goes right to there and what this matrix a does when you multiply it is it produces a new vector Y which is in the direction v 2 1 2 3 4 5 1 2 you know right about there or something like this so big deal you transform one vector to another so one way to think about this process is that what you actually did is you took this vector X you rotated it and then you stretched it and in fact any kind of process like this what a really does is it rotates and stretches vectors that’s all rotation and stretching so and I’ve shown you this so one way to think about it is if I again just to show you this let me take this thing here let me draw sort of a ball the same radius here as this thing here and you can see what it did it rotated by some angle theta 2 here and then you stretched it out a little bit so are there matrices for instance that capture these two fundamental idea is of rotation and stretching well if you want to rotate any matrix by an angle theta then there’s this very well-known matrix it’s called the rotation matrix this is in two dimensions and here it is let me write it down that’s it this matrix here rotates any vector by an angle theta okay so that is what this represents a rotation by theta all right now stretching is something different just all you need to do is think about a matrix I want to take a matrix now and stretch this vector okay well an easy way to do that is just to create the following matrix that’s it where alpha is your stretching okay so one way to think about a is that a itself is made up of some combination of rotation and stretching okay so a little bit of this matrix plus a little bit of this in this case here there’s some angle theta you rotated it through and then you stretched it so alpha is bigger than one so by the way just to see how this works on this so suppose I wanted to stretch this vector here by a factor of two make it twice as long then I can make alpha is two and then I’d get a new vector two two zero zero one three if you do this multiplication right you take this times this is two zero and then six right so it’s the vector two six well the vector 2 six is just twice as long sit so you can see that this thing will just stretch if alpha is bigger than one it stretches it if alpha is less than one it compresses it if alpha is zero it makes it zero of length zero okay so these are kind of fundamental ideas to have in your head that when you manipulate a vector with a matrix what you’re actually doing is nothing more than rotating stretching its it okay all right so this starts getting us to the idea of the singular value decomposition in particular we want to think about what happens to a circle under a matrix multiplication okay so let’s go ahead and take some kind of circle and in some coordinate system let’s say I can represent this with some orthogonal components b1 b2 and this is by the way in two dimensions but you can think about going to higher dimensions in fact so this is two dimensions and we want to think about n dimensions as a generalization so think about this as a circle in two dimensions in three dimensions it’s a sphere in four dimensions or five or six or more they’re called hyper spheres okay but it’s the same idea as this and then I asked the following question if I take a matrix a which is some kind of matrix which is an M by n matrix let me write it down here so I can get all my notation correctly to what I want so this is just an element of a M by n matrix I can ask the following question what happens to a sphere under this matrix operation in this case here this is since of two dimensions it’s not going to be M by n it’s going to be a two dimensional matrix like what happens these vectors when you hit it with a matrix multiply let’s take this out for a minute and what does happen well I just showed you what happens to a vector let’s come back to the other board for a moment you give me a matrix a and I ask what does it do it a vector what it does to a vector is it rotates and then either stretches or compresses it that’s it okay that’s what the matrix a does to an individual vector by the way it takes any vector and it rotates it by the same amount and stretching is the same amount okay it’s linear so it’s not like it acts differently on different vectors for every vector it rotates it by certain amount stretches it by certain amount so what happens to the image of a circle or more generally to a hyper circle or hyper sphere in these dimensions so I’m going to work in some sphere let’s call this a some sphere s and I’m going to hit this thing with a matrix a I’m going to ask what happens to that well what it’s going to do is going to rotate the sphere and stretch it well what happens if you take a sphere and you stretch it it becomes an ellipse so this thing here generically under the stretching process might becomes an ellipse okay so you went from a sphere to ellipse there was some rotation and then how do you quantify an ellipse what are the key factors in thinking about representing an ellipse typically what we think about is and you learn this very early on about ellipses there is these the major axis and the Minor axis so I can think about there’s my major axis there’s my minor axis actually let me draw it consistent with my notes okay major and minor axis and what I can do is think oh those are accordant a new coordinate system for me so I started off with the coordinate system over here orthogonal directions v1 and v2 and two dimensions of like this but remember I’m thinking about this as sort of a really in my hire generalization is I have an N dimensional sphere and what I did is I transformed it by a matrix multiply and what it did all the multiplication does is it rotates and stretches get that’s it it’s all matrix multiply does so I get into this space here where now I can say well let’s suppose I have some unit vectors along this direction in this direction the unit vector along this direction let’s call that u1 the unit direction along here is u2 and the distance along there I can think about well then this whole thing is some parameter Sigma 1 times u 1 this is Sigma 2 by u 2 so you want in you two are unit vectors they tell me which direction it’s going in Sigma 1 and Sigma 2 tells me how much how much in that direction I’m going okay so for convenience to think about this stretching operation remember a is an M by n matrix and now what I do over here is I have u 1 and u 2 but more generally this n dimensional sphere takes me to an n-dimensional what I call it whatever it’s called a hyper ellipse okay let me make this arrow a little more pointy alright so I started off in a vector space spanned by v1 v2 all the way to VN and I ended up in a new vector space u1 u2 u3 all the way to U of n ok so this is generically what happens that’s if a is full rank what I mean by that is you know you could always imagine if this is rank deficient in other words if I think about the number of rows or columns that are linearly independent then I could imagine a case where I act on this and I go to a smaller dimensional space just because this thing only acts in certain dimensions is it work ok so I have this new representation of orthogonal sets and in each direction there is the amount of stretch in that direction so these are unit vectors orthonormal and these are your stretching factor so there you go I took a sphere and under the matrix operation it stretches with some rotation into a new set of coordinates which the stretching factors and those coordinates are given by these singular these values here so these are the principal axes so the one way to think about this is these use these are your principal axes ok or principal semi-axes and the stretching factors are going to be call the singular values ok so it’s really important to try to understand this sort of an a fundamental point of view hopefully hopefully this kind of makes sense it’s just it’s just matrix multiplication all you do is you took a vector or took a set of vectors you rotated them you stretch them that’s it ok so that’s one way to think about it and again here it is here is the main idea take a vector when you multiply this thing you rotate your stretch okay that’s what you’re thinking about doing here in a simple 2x2 example and all you’re doing is saying well instead of 2 by 2 let’s go to n by n and let’s not just take a single vector but a whole you know set of basis vectors for this system into what happens in this new stretch coordinate system and this is it ok so this is the idea you go from one vector space here V 1 to V n under matrix multiplication by a you get to a new vector space which is just now you’re living on this stretch and rotate it ellipse we’re now you want to U of n or your basis factors there the unit vectors there tell you the directions this is now your new XYZ coordinate system that’s orthogonal to each other and Sigma 1 through Sigma N tell you how they’ve been stretched by this specific matrix a ok all right so let’s let’s write this down more formally when you think about this thing taking the a you’re going to take this a and multiply by V you’re going to start creating the structure you want to play with okay so let’s come over here and represent this okay I’m going to switch pins see if this one’s a little darker so what I want to do is think about the matrix of a acting on one of these matrices let’s say V 1 and it should produce Sigma 1 u 1 in other words take a act on V what does it do it rotates and stretches to a new vector u of length Sigma 1 remember U is a unit vector it’s length is 1 so you need the Sigma 1 there now the first thing I want to point out about this is doesn’t that look a little bit like an eigenvalue problem right usually the eigenvalue problem is written down like this so you kind of have a lot of the same elements you have a matrix a you have a vector is equal to some constant in this case the constant B lambda would be Sigma 1 but now here’s the big difference you have au 1 normally an eigenvalue problem would be V 1 and V 1 over here now you can have a different vector over there v1 produces u1 okay so it’s not one of these but there’s definitely a very intimate relationship between this and the eigenvalue problem which I will show you in just a moment so this is how it acts on a single vector so you can imagine well how does it do on all the vectors well here’s how it does on all the vectors each one does this the V of J produces the U of J times Sigma J a really nice way to write this is if I write all the equations down at once is the following so I’m going to write all these there’s n of these equations so let me try to write it in a form that kind of makes sense I consider the matrix a and it’s multiplying what well v1 and then v2 and v3 so let me think about this v1 and v2 v3 all the way to V of n okay so first thing here if you remember a itself is a matrix of M by N and to do this multiplication V itself is n by n here in fact look at this the columns of this matrix are v1 v2 v3 v4 all the way to view of n so this has n columns and there’s n rows so this thing here should be a n by n so that’s this left side is equal to well in the first case here let me write in this way here so it’s equal to Sigma J use of J so first I’m gonna put in here u 1 you too all the way to U of n times now I have a diagonal matrix with Sigma 1 Sigma 2 all the way to Sigma n 0 everywhere else so for instance think about the first row of this equation it’s a times V 1 8 times V 1 produces u 1 times Sigma 1 that’s that first equation the second row a times V 2 produces u 2 times Sigma 2 it’s the second of these equations and so forth so this here is a nice representation of all of these together ok so this set of equations can be very conveniently represented this way you take all the V vectors you stack them on columns take all the u vectors stack them and columns this is a diagonal matrix where the Sigma is along the diagonals and so one way to think about this is just say well if I have that then this thing here is the matrix a times let’s call this a make vector matrix V is equal to call this matrix u hat I’ll tell you why in a little bit and Sigma hat okay all I’ve done is written this set of equations all together here like this and this is how you would write them in a very short hand way in a matrix multiply way the matrix a times V where V the calls V are all the V vectors you had before is equal to matrix u which is all the new vectors in this hyper ellipse space times Sigma which are these singular values the stretching factors a couple things I want to point out I’m going to assume that these V’s are basically orthogonal orthonormal set right that’s kind of how he drew it let’s come back over to here right so the v1 and v2 were these orthogonal directions unit length that’s why it’s a circle so these are orthogonal coordinates that get transferred to here to another set of orthogonal coordinates u 1 and 2 u 1 and u 2 remember our unit length and are orthogonal to each other so I went from one ortho Northam orthonormal basis to another orthonormal basis okay so what you can think about is all you did with this matrix a at least in terms of producing use is that it was a rotation that’s the rotation piece when you go from these to use remember a produces rotation and stretching all the stretching is picked up by the Sigma all the rotations picked up by the use so one way to think about this matrix here then is to say well the v’s this is a like a rotation matrix this is also like a rotation matrix and this is your stretching now there’s a fancy name for a rotation matrix it’s called a unitary transformation and if these are orthonormal components here and if and we think about this then is a rotation matrix then what ends up happening there’s some special properties of this matrix which is the inverse of the matrix is the same as its transpose so in that case the big deal about a unitary unitary unitary matrix is that V minus 1 is equal to V star which is the complex conjugate transpose okay so that’s the way you want to think about it this is rotation matrix and if it’s unit or unitary this holds same thing with this inverse of that matrix is transpose complex conjugates so actually finding the inverse is trivial you just simply transpose and anywhere you see in complex I turn it to minus I that’s it so you can easily get your inverse for the matrices okay all right so hopefully everybody’s good at this point it is very important that you understand from this formula here or this this formula here for this n of these right I’m acting on each of the N directions of V to produce new and directions in you with a straight scaling factor stretching or compression and then if I combine all in Quay shion’s together generically it looks like this which in matrix form is right there okay kind of convenient so

let’s go back over here talk about what this means so let’s write this down a V is equal to u hat Sigma hat now what I’m going to do with this is to multiply both sides on the right times V inverse so a V V inverse that’s one that’s the identity so this is equal to a times I which is equal to a so that’s the left side the right side is U hat Sigma hat B minus one but if you remember the inverse is the same as the complex conjugate transpose V since okay so that gives you u hat Sigma hat V star this is called the reduced singular value decomposition so what does it say my matrix a what do matrices do remember what do matrices do they rotate and they stretch that’s all so how do I get the rotations and stretchings of this matrix a correctly well a is a rotation times a stretching times a rotation so the idea is that this decomposition exists into these three component parts okay so I’ve replaced one matrix by three okay but this is kind of important so let me try to draw graphically what this thing looks like the matrix a if you remember a itself is a M by n okay is equal to u times Sigma times the star okay so that’s kind of the generic description there of this matrix so this here is some kind of this is a an M by n here and all this means it’s a set of complex numbers it’s n by n this thing here is also this is actually M by N and then this thing here is oops it’s an element not a dove this thing here is M by n and or actually M by M okay and by N and that thing there is M by n okay actually excuse me let’s end by n as well okay this is in the reduced form and remember this thing is diagonal so only has entries along here this diagonal term but this can be full this is fullness in matrix a so this is what’s called the reduced SVD the more standard way that people often work think about the SVD is to say okay I have this M by n matrix this is M rows and columns so in some sense it’s like an underdetermined matrix okay so at most I have n columns it’s only going to span an N dimensional space one thing I could do is add some what are called silent rows so I take my rows that I have and I add so remember I have here n of them and I add M minus n so that this thing here now is M by M it’s full rank square matrix does it matter if I add these remember these are n orthogonal directions and all I’m saying is well okay if there’s n orthogonal directions I can make up and minus in other orthogonal directions that are thuggin ‘el to these doesn’t cost me anything I can do that and then I can also stretch my Sigma matrix accordingly so there’s my singular values the rest down here are all zeros so this was Sigma bar this was V bar and then V itself is here sorry this was V hat that was upat here Sigma hat V star this is now the new U which is M by n M by M and then now this Sigma here which is not Sigma bar it’s an element of and by N and then this V Star is an element it’s still n by n okay this is called the singular value decomposition okay so you take a matrix a you represent it as some matrix u times singular values C which are the stretching factors times V V star which is the complex conjugate transpose or the inverse V which is n by n M by M M by n okay now normally the way you order this too is that when you do the singular value decomposition it’s always ordered in the following way biggest to smallest all singular values are equal through greater than zero there are no negative singular values they’re all positive numbers positive real numbers ordered biggest to smallest so when you think about this biggest to smallest on down the line there okay so this tells you the stretching in every single direction so you take the sphere and if you transform it it’s like stretching it in some directions and how you rotate is telling you is being basically dictated by these two matrices and how you stretch is being dictated by this one that’s it now there’s a theorem concerning this that I think is very important to write down so let me write it down and this is also going to be a big difference between an eigenvalue decomposition in this okay every matrix a has a singular value decomposition okay so full stop for a moment a lot of matrices you try to decompose them like we’ve talked about Lu decomposition eigenvalue decomposition those aren’t guaranteed to work for every matrix if you have a matrix that’s a singular for instance Lu won’t work if if you’re doing I in value decompositions similar kind of things it only works in certain cases SVD always works always always always okay there’s never an exception you can always do a singular value decomposition moreover the singular values given by this set Sigma J’s are uniquely determined okay and if a is square okay the Sigma J are distinct okay and the singular value and then also the singular vectors you of J’s and V of J’s are also unique up to a complex time okay this thing always works it always produces for you singular values that are positive and order from biggest to smallest and it always produces you those are unique the same thing with the unique eigenvectors or sort of unique singular vectors U and V okay so the question then comes how do you compute from a matrix a this matrix U the matrix V and the matrix C so in other words remember you’re saying my matrix a always has this decomposition and the question is how do i compute these things what’s the formula to being able to compute this and here is where we show you

How SVD relates to eigenvalues and eigenvectors

okay so you think about the following a transpose a one thing to think about if I want to compute this SVD this is where this is going to go towards well a transpose a well a itself right is U Sigma Sigma V Star and then I have u Sigma V Star and I’m taking the transpose of that well the transpose switch switches the orders okay and so what I end up getting if I if I do this not only switches the order but I’m taking the transpose well actually it also takes stars on stars it and put stars here so then you get something like this V Sigma u star that’s what you get when you transpose this thing here it switches the order of multiplication and then it transpose as these but that star really means transpose so you transpose that and you transpose a transpose a transpose just gives you back the V itself times u Sigma V star but if you remember u star times u well u star is basically because it’s unit unitary matrix it’s a rotation matrix U star is equivalent to u inverse u inverse times use one so what do you get V simha one so I’m going to be star well this is one so you just get Sigma squared there okay there’s that to keep in mind and then I can say okay that’s one observation so let’s take a transpose a times V well that’s this is a transpose AV Sigma squared times the star times V but what is V Star times V 1 because the transpose of this unitary matrix is V to the minus 1 this times this is 1 and so you end up getting here V Sigma squared is a transpose a v and this is an eigenvalue problem this is ax equals lambda X you’re right in our standard way to think about eigenvalues so here the lambda is this Sigma squared the X are these vectors here and the a now is this matrix there so it’s not a value problem so if I solve this eigenvalue problem what do I get the the eigenvalues lambda are like the lambda J’s are like the Sigma squared J’s so that’s great

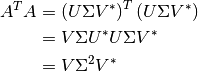
so if I can find the eigenvalues they’re going to be equivalent to Sigma J Squared’s and the eigenvectors are v that’s how I get V how about I get you if you get you the following way a times a transpose well a times a transpose is U Sigma V Star times u Sigma V star transpose which is u Sigma V star remember the transpose here flips you order and transpose is so that gives you a V Sigma u star P star times V is one you get u Sigma squared U star multiplying out both sides by you if you multiply both sides by you what you end up getting the following that’s one so you get a a transpose U is equal to u Sigma squared I can value problem same eigen values as here so the singular matrix Sigma is the same for both but notice when you solve this eigenvalue problem of a a transpose versus h kram chose a what you end up getting are the eigenvectors are the eigenvectors give you the matrix u this eigenvalue problem this is how you get you write you solve for always all the eigen values one other thing to note is that you always know you can solve this because by doing a a transpose what you’ve effectively done by doing this is this matrix here now becomes what’s called self adjoint or hermitian which guarantees that in fact the eigenvalues are real and positive and distinct which you already known to be the case for these ok so you get the eigen vectors you heigen vectors of this eigenvalue pump gives you u you can also get your eigen values which gives you your singular values and from this one over here you can get onion vectors of V okay so that’s how you would compute this U and V to begin with now so far all we’ve talked about this is essentially this decomposition says what I can do is a matrix a what do I know what to do I know that what it does is it rotates and stretches and in particular we come back over here real quick to finish off the matrix you want to acts on a vector it rotates stretches rotates okay this is from the simple example I gave at the beginning of class you know that’s all it does rotates and stretches so here’s a formula for doing it you’re always guaranteed to do this but what you can do with this thing is magic so what we’re going to learn in the next couple of lectures is what this thing can do for you in terms of solving data analysis problems and that will be the topic for the follow-up lectures on a single single value decomposition Up next

Non-negative matrix factorization (NMF)

https://www.quora.com/What-is-Maximum-Margin-Matrix-Factorization

Lee DDSeung HS (1999) Learning the parts of objects by non-negative matrix factorization Nature 401:788–791.https://doi.org/10.1038/44565 https://pubmed.ncbi.nlm.nih.gov/10548103/

In matrix factorization , you try to approximate X^∈Rn×m of a matrix X in mathbb{R}{n times m}^ i.e X^≈X=UVT where U∈Rk×m and VT∈Rk×m . This approximation is done by minimizing an error criteria which for example could be the Frobenius difference between the original matrix and approximate one.

Srebro [1] propose a low trace norm constraint instead of constraining the rank of the matrix. In contrast to use Frobenius norm in low-rank settings, they propose the Hinge loss (The authors work with discrete values). The objective function turns to be

X^=λ||X^||sigma+∑i,j∈XLh(X,X^)

where λ>0 is a parameter for approximation between regularization error and regularization term. By following [1] Srebro shows the objective function can be changed to

X^=λ2(||U||2F+||V||2F)+∑i,jh(X,uivTj) .

Solving the above equation by Gradient Descent is still hard so what you do is you change the loss function to the smooth hinge loss making the objective function differentiable [2].

[1]Maximum margin matrix factorization N. Srebro, J. D. M. Rennie, and T. Jaakkola. [2]Fast Maximum Margin Matrix Factorizationfor Collaborative Prediction Jason Rennie and Nathan Srebro